Routing in delay-tolerant networking
Routing in delay-tolerant networking concerns itself with the ability to transport, or route, data from a source to a destination is a fundamental ability all communication networks must have. Delay- and disruption-tolerant networks (DTNs), are characterized by their lack of connectivity, resulting in a lack of instantaneous end-to-end paths. In these challenging environments, popular ad hoc routing protocols such as AODV[1] and DSR[2] fail to establish routes. This is due to these protocols trying to first establish a complete route and then, after the route has been established, forward the actual data. However, when instantaneous end-to-end paths are difficult or impossible to establish, routing protocols must take to a "store and forward" approach, where data is incrementally moved and stored throughout the network in hopes that it will eventually reach its destination[3][4][5]. A common technique used to maximize the probability of a message is successfully transferred is to replicate many copies of the message in hopes that one will succeed in reaching its destination[6].
Contents |
Routing considerations
There are many characteristics DTN protocols, including routing, must take into consideration. A first consideration is if information about future contacts is readily available. For example, in interplanetary communications, many times a planet or moon is the cause of contact disruption, and large distance is the cause of communication delay. However, due to the laws of physics, it is possible to predict the future in terms of the times contacts will be available, and how long they will last. These types of contacts are known as scheduled or predictable contacts[7]. On the contrary, in disaster recovery networks the future location of communicating entities, such as emergency responders, may not be known. These types of contacts are known as intermittent or opportunistic contacts.
A second consideration is if mobility can be exploited and, if so, which nodes are mobile. There are three major cases, classifying the level of mobility in the network. First, it is possible that there are no mobile entities. In this case, contacts appear and disappear based solely on the quality of the communication channel between them. For instance, in interplanetary networks, large objects in space, such as planets, can block communicating nodes for a set period of time. Second, it is possible that some, but not all, nodes in the network are mobile. These nodes, sometimes referred to as Data Mule[8][9], are exploited for their mobility. Since they are the primary source of transitive communication between two non-neighboring nodes in the network, an important routing question is how to properly distribute data among these nodes. Third, it is possible that the vast majority, if not all, nodes in the network are mobile. In this case, a routing protocol will most likely have more options available during contact opportunities, and may not have to utilize each one[3][10][11][12]. An example of this type of network is a disaster recovery network where all nodes (generally people and vehicles) are mobile[13]. A second example is a vehicular network where mobile cars, trucks, and buses act as communicating entities[3].
A third consideration is the availability of network resources. Many nodes, such as mobile phones, are limited in terms of storage space, transmission rate, and battery life. Others, such as buses on the road, may not be as limited. Routing protocols can utilize this information to best determine how messages should be transmitted and stored to not over-burden limited resources. As of April 2008, only recently has the scientific community started taking resource management into consideration, and this is still an active area of research.
Routing protocol classifications
While there are many characteristics of routing protocols, one of the most immediate ways to create a taxonomy is based on whether or not the protocol creates replicas of messages. Routing protocols that never replicate a message are considered forwarding-based, whereas protocols that do replicate messages are considered replication-based. This simple, yet popular, taxonomy was recently used by Balasubramanian et al. to classify a large number of DTN routing protocols[10].
There are both advantages and disadvantages to each approach, and the appropriate approach to use is probably dependent on the scenario at hand. Forwarding-based approaches are generally much less wasteful of network resources, as only a single copy of a message exists in storage in the network at any given time[7][14]. Furthermore, when the destination receives the message, no other node can have a copy. This eliminates the need for the destination to provide feedback to the network (except for, perhaps, an acknowledgments sent to the sender), to indicate outstanding copies can be deleted. Unfortunately, forwarding-based approaches do not allow for sufficient message delivery rates in many DTNs[11]. Replication-based protocols, on the other hand, allow for greater message delivery rates[3], since multiple copies exist in the network, and only one (or in some cases, as with erasure coding, a few) must reach the destination. However, the tradeoff here is that these protocols can waste valuable network resources[12]. Furthermore, many flooding-based protocols are inherently not scalable. Some protocols, such as Spray and Wait[11], attempt to compromise by limiting the number of possible replicas of a given message.
It is important to note that the vast majority of DTN routing protocols are heuristic-based, and non-optimal. This is due to optimality being, in the general DTN case, NP-hard[10]. More specifically "online algorithms without complete future knowledge and with unlimited computational power, or computationally limited algorithms with complete future knowledge, can be arbitrarily far from optimal"[10].
Replication-based routing
Replication-based protocols have recently obtained much attention in the scientific community, as they can allow for substantially better message delivery ratios than in forwarding-based protocols. These types of routing protocols allow for a message to be replicated; each of the replicas, as well as the original message itself, are generally referred to as message copies or message replicas. Possible issues with replication-based routing include:
- network congestion in clustered areas,
- being wasteful with network resources (including bandwidth, storage, and energy), and
- network scalability.
Since network resources may quickly become constrained, deciding which messages to transmit first and which messages to drop first play critical roles in many routing protocols.
Epidemic routing
Epidemic routing[6] is flooding-based in nature, as nodes continuously replicate and transmit messages to newly discovered contacts that do not already possess a copy of the message. In the most simple case, epidemic routing is flooding; however, more sophisticated techniques can be used to limit the number of message transfers. Epidemic routing has its roots in ensuring distributed databases remain synchronized, and many of these techniques, such as rumor mongering, can be directly applied to routing.
PRoPHET routing protocol
Epidemic routing is particularly resource hungry because it deliberately makes no attempt to eliminate replications that would be unlikely to improve the delivery probability of messages. This strategy is effective if the opportunistic encounters between nodes are purely random, but in realistic situations, encounters are rarely totally random. Data Mules (mostly associated with a human) move in a society and accordingly tend to have greater probabilities of meeting certain Mules than others. The Probabilistic Routing Protocol using History of Encounters and Transitivity (PRoPHET) protocol uses an algorithm that attempts to exploit the non-randomness of real-world encounters by maintaining a set of probabilities for successful delivery to known destinations in the DTN (delivery predictabilities) and replicating messages during opportunistic encounters only if the Mule that does not have the message appears to have a better chance of delivering it. This strategy was first documented in a paper from 2003 [15].
An adaptive algorithm is used to determine the delivery predictabilities in each Mule. The Mule M stores delivery predictabilities P(M,D) for each known destination D. If the Mule has not stored a predictability value for a destination P(M,D) is assumed to be zero. The delivery predictabilities used by each Mule are recalculated at each opportunistic encounter according to three rules:
- When the Mule M encounters another Mule E, the predictability for E is increased:
P(M,E)new = P(M,E)old + (1 - P(M,E)old) * Lencounter where Lencounter is an initialisation constant. - The predictabilities for all destinations D other than E are 'aged':
P(M,D)new = P(M,D)old * γK where γ is the aging constant and K is the number of time units that has elapsed since the last aging. - Predictabilities are exchanged between M and E and the 'transitive' property of predictability is used to update the predictability of destinations D for which E has a P(E,D) value on the assumption that M is likely to meet E again:
P(M,D)new = P(M,D)old + (1 - P(M,D)old) * P(M,E) * P(E,D) * β where β is a scaling constant.
The protocol has been incorporated into the reference implementation maintained by the IRTF DTN Research Group and the current version is documented in an Internet Draft[16]. The protocol has been trialled in real world situations during the Sámi Network Connectivity (SNC) project and is being further developed during the EU Framework Programme 7 project Networking for Communications Challenged Communities (N4C).
MaxProp
MaxProp[3] was developed at the University of Massachusetts, Amherst and was, in part, funded by DARPA and the National Science Foundation. The original paper is found in the IEEE INFOCOM 2006 conference. MaxProp is flooding-based in nature, in that if a contact is discovered, all messages not held by the contact will attempt to be replicated and transferred. The intelligence of MaxProp comes in determining which messages should be transmitted first and which messages should be dropped first. In essence, MaxProp maintains an ordered-queue based on the destination of each message, ordered by the estimated likelihood of a future transitive path to that destination.
MaxProp core
To obtain these estimated path likelihoods, each node maintains a vector of size 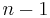 (where
(where  is the number of nodes in the network) consisting of the likelihood the node has of encountering each of the other nodes in the network. Each of the
is the number of nodes in the network) consisting of the likelihood the node has of encountering each of the other nodes in the network. Each of the 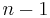 elements in the vector is initially set to
elements in the vector is initially set to 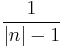 , meaning the node is equally likely to meet any other node next. When the node meets another node,
, meaning the node is equally likely to meet any other node next. When the node meets another node,  , the
, the 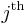 element of its vector is incremented by 1, and then the entire vector is normalized such that the sum of all entries add to 1. Note that this phase is completely local and does not require transmitting routing information between nodes.
element of its vector is incremented by 1, and then the entire vector is normalized such that the sum of all entries add to 1. Note that this phase is completely local and does not require transmitting routing information between nodes.
When two nodes meet, they first exchange their estimated node-meeting likelihood vectors. Ideally, every node will have an up-to-date vector from every other node. With these n vectors at hand, the node can then compute a shortest path via a depth-first search where path weights indicate the probability that the link does not occur (note that this is 1 minus the value found in the appropriate vector). These path weights are summed to determine the total path cost, and are computed over all possible paths to the destinations desired (destinations for all messages currently being held). The path with the least total weight is chosen as the cost for that particular destination. The messages are then ordered by destination costs, and transmitted and dropped in that order.
MaxProp additions
In conjunction with the core routing described above, MaxProp allows for many complementary mechanisms, each helping the message delivery ratio in general. First, acknowledgements are injected into the network by nodes that successfully receive a message (and are the final destination of that message). These acknowledgements are 128-bit hashes of the message that are flooded into the network, and instruct nodes to delete extra copies of the message from their buffers. This helps free space so outstanding messages are not dropped as often. Second, packets with low hop-counts are given higher priority. This helps promote initial rapid message replication to give new messages a "head start". Without this head start, newer messages can be quickly starved by older messages, since there are generally less copies of new messages in the network. Third, each message maintains a "hop list" indicating nodes it has previously visited to ensure that it does not revisit a node.
RAPID
RAPID[10], which is an acronym for Resource Allocation Protocol for Intentional DTN routing, was developed at the University of Massachusetts, Amherst. It was first introduced in the SIGCOMM 2007 publication, DTN Routing as a Resource Allocation Problem. The authors of RAPID argue as a base premise that prior DTN routing algorithms incidentally effect performance metrics, such as average delay and message delivery ratio. The goal of RAPID is to intentionally effect a signal routing metric. At the time of publication, RAPID has been instrumented to intentionally minimize one of three metrics: average delay, missed deadlines, and maximum delay.
RAPID protocol
The core of the RAPID protocol is based around the concept of a utility function. A utility function assigns a utility value, 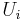 , to every packet
, to every packet  , which is based on the metric being optimized.
, which is based on the metric being optimized. 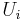 is defined as the expected contribution of packet
is defined as the expected contribution of packet  to this metric. RAPID replicates packets first that locally result in the highest increase in utility. For example, assume the metric to optimize is average delay. The utility function defined for average delay is
to this metric. RAPID replicates packets first that locally result in the highest increase in utility. For example, assume the metric to optimize is average delay. The utility function defined for average delay is 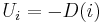 , basically the negative of the average delay. Hence, the protocol replicates the packet that results in the greatest decrease in delay. RAPID, like MaxProp, is flooding-based, and will therefore attempt to replicate all packets if network resources allow.
, basically the negative of the average delay. Hence, the protocol replicates the packet that results in the greatest decrease in delay. RAPID, like MaxProp, is flooding-based, and will therefore attempt to replicate all packets if network resources allow.
The overall protocol is composed of four steps:
- Initialization: Metadata is exchanged to help estimate packet utilities.
- Direct Delivery: Packets destined for immediate neighbors are transmitted.
- Replication: Packets are replicated based on marginal utility (the change is utility over the size of the packet).
- Termination: The protocol ends when contacts break or all packets have been replicated.
Spray and Wait
Spray and Wait is a routing protocol that attempts to gain the delivery ratio benefits of replication-based routing as well as the low resource utilization benefits of forwarding-based routing. Spray and Wait was developed by researchers at the University of Southern California. It was first presented at the 2005 ACM SIGCOMM conference, under the publication "Spray and Wait: An Efficient Routing Scheme for Intermittently Connected Mobile Networks". Spray and Wait achieves resource efficiency by setting a strict upper bound on the number of copies per message allowed in the network.
Spray and Wait protocol overview
The Spray and Wait protocol is composed of two phases: the spray phase and the wait phase. When a new message is created in the system, a number  is attached to that message indicating the maximum allowable copies of the message in the network. During the spray phase, the source of the message is responsible for "spraying", or delivery, one copy to
is attached to that message indicating the maximum allowable copies of the message in the network. During the spray phase, the source of the message is responsible for "spraying", or delivery, one copy to  distinct "relays". When a relay receives the copy, it enters the wait phase, where the relay simply holds that particular message until the destination is encountered directly.
distinct "relays". When a relay receives the copy, it enters the wait phase, where the relay simply holds that particular message until the destination is encountered directly.
Spray and Wait versions
There are two main versions of Spray and Wait: vanilla and binary. The two versions are identical except for how the  copies reach
copies reach  distinct nodes during the spray phase. The simplest way to achieve this, known as the vanilla version, is for the source to transmit a single copy of the message to the first
distinct nodes during the spray phase. The simplest way to achieve this, known as the vanilla version, is for the source to transmit a single copy of the message to the first 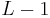 distinct nodes it encounters after the message is created.
distinct nodes it encounters after the message is created.
A second version, referred to as Binary Spray and Wait. Here, the source starts, as before, with  copies. It then transfers
copies. It then transfers 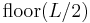 of its copies to the first node it encounters. Each of these nodes then transfers half of the total number of copies they have to future nodes they meet that have no copies of the message. When a node eventually gives away all of its copies, except for one, it switches into the wait phase where it waits for a direct transmission opportunity with the destination. The benefit of Binary Spray and Wait is that messages are disseminated faster than the vanilla version. In fact, the authors prove that Binary Spray and Wait is optimal in terms of minimum expected delay among all Spray and Wait schemes, assuming node movement is IID.
of its copies to the first node it encounters. Each of these nodes then transfers half of the total number of copies they have to future nodes they meet that have no copies of the message. When a node eventually gives away all of its copies, except for one, it switches into the wait phase where it waits for a direct transmission opportunity with the destination. The benefit of Binary Spray and Wait is that messages are disseminated faster than the vanilla version. In fact, the authors prove that Binary Spray and Wait is optimal in terms of minimum expected delay among all Spray and Wait schemes, assuming node movement is IID.
References
- ^ C. E. Perkins and E. M. Royer. Ad-hoc on-demand distance vector routing. In The Second IEEE Workshop on Mobile Computing Systems and Applications, February 1999.
- ^ D. B. Johnson and D. A. Maltz. Mobile Computing, chapter Dynamic source routing in ad hoc wireless networks, pages 153–181. Kluwer Academic Publishers, February 1996.
- ^ a b c d e John Burgess, Brian Gallagher, David Jensen, and Brian Neil Levine. MaxProp: Routing for vehicle-based disruption-tolerant networks. In Proc. IEEE INFOCOM, April 2006.
- ^ Philo Juang, Hidekazu Oki, Yong Wang, Margaret Martonosi, Li Shiuan Peh, and Daniel Rubenstein. Energy-efficient computing for wildlife tracking: design tradeoffs and early experiences with zebranet. SIGOPS Oper. Syst. Rev., 36(5):96–107, 2002.
- ^ Augustin Chaintreau, Pan Hui, Jon Crowcroft, Christophe Diot, Richard Gass, and James Scott. Impact of human mobility on opportunistic forwarding algorithms. IEEE Transactions on Mobile Computing, 6(6):606–620, 2007.
- ^ a b Amin Vahdat and David Becker. Epidemic routing for partially connected ad hoc networks. Technical Report CS-2000-06, Department of Computer Science, Duke University, April 2000.
- ^ a b Sushant Jain, Kevin Fall, and Rabin Patra. Routing in a delay-tolerant network. In Proc. ACM SIGCOMM, 2004.
- ^ Jea D., Somasundara A. A, and Srivastava M. B. Multiple Controlled Mobile Elements (Data Mules) for Data Collection in Sensor Networks. In Proc. IEEE/ACM International Conference on Distributed Computing in Sensor Systems (DCOSS), June 2005.
- ^ Rahul C. Shah, Sumit Roy, Sushant Jain, and Waylon Brunette. Data MULEs: Modeling a Three-tier Architecture for Sparse Sensor Networks. In Proc. IEEE SNPA Workshop, May 2003.
- ^ a b c d e Aruna Balasubramanian, Brian Neil Levine, and Arun Venkataramani. DTN routing as a resource allocation problem. In Proc. ACM SIGCOMM, August 2007.
- ^ a b c Thrasyvoulos Spyropoulos, Konstantinos Psounis, and Cauligi S. Raghavendra. Spray and wait: An efficient routing scheme for intermittently connected mobile networks. In WDTN ’05: Proceeding of the 2005 ACM SIGCOMM workshop on Delay-tolerant networking, 2005.
- ^ a b Thrasyvoulos Spyropoulos, Konstantinos Psounis, and Cauligi S. Raghavendra. Spray and focus: Efficient mobility-assisted routing for heterogeneous and correlated mobility. In Fifth Annual IEEE International Conference on Pervasive Computing and Communications Workshops, 2007.
- ^ Samuel C. Nelson, Albert F. Harris, and Robin Kravets. Event-driven, role-based mobility in disaster recovery networks. In CHANTS 07: Proceedings of the second workshop on Challenged Networks, 2007.
- ^ Dan Henriksson, Tarek F. Abdelzaher, and Raghu K. Ganti. A caching-based approach to routing in delay-tolerant networks. In Proceedings of 16th International Conference on Computer Communications and Networks, 2007. ICCCN 2007, 2007.
- ^ A. Lindgren, A. Doria, and O. Scheln. Probabilistic routing in intermittently connected networks. In Proceedings of the Fourth ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc 2003), 2003.
- ^ A. Lindgren and A. Doria, Probabilistic Routing Protocol for Intermittently Connected Networks, Internet Draft - http://tools.ietf.org/html/draft-irtf-dtnrg-prophet, February 2010